From Laws to Conservation: Newton’s Grammar of Motion

Motion tells stories. Kinematics describes the plot—where things go, how fast, how curves bend. Dynamics asks the deeper question: what makes the plot change? Newton’s answer was radical in its simplicity. Three concise statements—call them axioms—turn scattered observations into a grammar.

In this chapter we keep that grammar human: plain language first, pictures before equations, and just enough mathematics to compute without losing the thread of meaning.

We will learn to draw clean free-body diagrams, to read the sum of F right arrow equals m a right arrow as a vector sentence about causes and changes, and to recognise two deeper patterns hiding in the details: energy is conserved when nothing in the laws depends on time, and momentum is conserved when nothing depends on where you are in space.

Symmetry whispers conservation; arrangement reveals it.

Bridge — From Patterns to Causes

Part 1 taught us to pay attention; Part 2 taught us to measure change. Now we cross a bridge from pattern to cause. It is perfectly possible for an object to glide across the floor at steady speed with no net push acting on it. That is not a contradiction; it is a clarification.

Velocity describes how position changes; acceleration describes how velocity changes. Only acceleration demands a cause. The cause we admit in classical mechanics is the net external force: the vector sum of every push and pull that the outside world exerts on the object you are analysing. The path from observation to explanation then runs through a simple rule: if velocity bends, there is a net force; if it does not, there is not.

The right mindset is investigative rather than muscular. Instead of asking “How hard should I push?” ask “What forces already exist here, and how are they arranged?” Often the better move is not more effort but a smarter configuration—sloping the ramp, reducing friction, aligning the pull with the likely motion. Dynamics rewards good setups.

Newton’s Three Laws

First law (Inertia). In the absence of a net external force, an object maintains its state of motion—either remaining at rest or continuing in a straight line at constant speed. This is not merely a property of objects; it is also a statement about frames of reference. Frames in which the first law holds without inventing extra forces are called inertial frames. A bus that lurches forward is not such a frame. When the coffee slides backwards on your seat, nothing “pulls it back”; rather, the bus floor surges forward beneath it while the cup tries to maintain its state. The cure is either to analyse in the ground frame, where roads are approximately inertial, or to include appropriate inertial (fictitious) forces if you insist on staying aboard the accelerating bus.

Second law (Acceleration). When a non-zero net external force acts on a body of constant mass, the body accelerates according to the sum of F right arrow equals m a right arrow. This is a vector equation. It speaks component-wise about how the forces along x, y, and z cause the corresponding accelerations. Mass measures resistance to change in velocity; given the same push, a lighter cart experiences a larger acceleration than a heavier one. Units tell the same story: one newton (N) equals one kilogram–metre per second squared, kg times normal m divided by normal s squared.

Third law (Action–Reaction). Forces occur in pairs, equal in magnitude and opposite in direction, and—crucially—acting on different bodies. When your hand presses the wall, the wall presses your hand. The two forces do not cancel on a single object; each belongs to a different free-body diagram. The third law keeps momentum accounting honest and builds bridges between interacting parts of a system. Together these three laws sketch a worldview: motions persist unless causes intervene, causes produce accelerations in proportion to their strength and inversely to inertia, and interactions are mutual.

Forces in the Wild

Forces are the means by which the world negotiates change. Near Earth the gravitational force on a mass m is its weight, W right arrow equals m g right arrow, directed downward with magnitude about 9.81 normal m divided by normal s squared times the mass. Weight is a force that depends on the surrounding field; mass is a property of the object itself and does not change if you carry the object to the Moon.

At solid boundaries the force you feel is the normal force, the push a surface exerts to prevent interpenetration. It is best thought of as a constraint that adjusts to the situation. Stand still on a level floor and the normal force happens to equal m g upward; lean on a wall and a horizontal normal appears to cancel your push; ride an elevator and the normal force becomes larger during upward acceleration and smaller when you accelerate downward.

There is no universal formula N equals m g; there is only the requirement that the surface supplies whatever is necessary (within its limits) to keep the contact geometry intact.

Friction is the texture of contact. When surfaces attempt to slide but have not yet done so, static friction responds just enough to oppose the would-be motion, up to a maximum F sub s comma max equals mu sub s N. Once sliding begins, kinetic friction tends to settle near F sub k equals mu sub k N and points opposite the motion relative to the surface.

A block on a gently tilted board will not move until the component of weight along the board, m g of sine theta, exceeds mu sub s N; beyond that angle it will slide, and then the relevant coefficient is mu sub k. This is why starting a heavy object can feel harder than keeping it moving.

Strings, ropes, and cables transmit tension, which pulls along their length and is the same throughout an ideal, massless rope passing over a frictionless pulley. Springs in their linear regime obey Hooke’s law, F right arrow equals negative k x right arrow: the displacement from equilibrium is a measure of how strongly the spring tries to restore itself.

Free-Body Diagrams — Reading a Situation

A free-body diagram (FBD) is a portrait of forces. The rule is simple: isolate the object of interest, cut it free from its environment, and replace every interaction with an explicit force vector acting on the object. Draw weight from the centre of mass pointing down. Draw normals at the contact surfaces, perpendicular to those surfaces. Add friction arrows along the surfaces, opposing relative motion or the intention to move. Include any applied pulls or pushes, tensions along strings, and spring forces along lines of stretch or compression. Only external forces belong; internal forces between parts of the same isolated object cancel and disappear from a single diagram.

On an inclined plane the diagram becomes eloquent. A block of mass m sits on a frictionless slope angled at theta. Gravity acts straight down, but it is convenient to choose axes parallel and perpendicular to the slope. Resolve the weight into m g of sine theta down the plane and m g of cosine theta into the plane. The surface supplies a normal force N equals m g of cosine theta that prevents interpenetration but does not impede motion along the surface. Along that direction, the net force is m g of sine theta, so the acceleration is a equals g of sine theta. No mystery—only geometry.

On a rough horizontal surface with a constant horizontal pull F, the story is different. Vertically, the normal force balances the weight, giving N equals m g for a level surface. Horizontally, kinetic friction subtracts mu sub k N from the applied pull. The remaining net force, F minus mu sub k m g, produces an acceleration a equals open paren F minus mu sub k m g close paren divided by m. If the pull just equals mu sub k m g, the acceleration vanishes and the cart glides at constant speed. The diagram tells the tale at a glance.

From Law to Number

Because the sum of F right arrow equals m a right arrow is a vector statement, it pays to choose axes that respect the arrangement. Align one axis with the likely motion or with a prominent surface, and resist solving everything at once. Compute components. Check units. A newton is kg times normal m divided by normal s squared, a joule is a newton–metre, and power measured in watts is joules per second. Dimensional analysis is a kind of grammar check: if the left-hand side of your equation is a force and the right-hand side is an energy, a silent mistake has crept in.

Often a quick scaling argument sharpens intuition. Double the mass while keeping the same pull, and the acceleration halves. Tilt the plane a little more and sine theta grows approximately like theta for small angles, so gentle tilts produce gentle accelerations. Replace wood with Teflon and the coefficient of friction falls; the same pull now buys more acceleration. Numbers come later; arrangement speaks first.

Gravity as an Example Law

Near Earth’s surface the gravitational field is nearly uniform, and we comfortably take g right arrow as constant over human-sized heights. For widely separated masses, Newton’s law of universal gravitation declares F sub g equals G of the fraction with numerator m sub 1 m sub 2 and denominator r squared, an attractive force directed along the line joining the masses. This single statement connects apples and planets. The same inverse-square rule that pulls a dropped key toward the floor shapes the elliptical dance of the Moon around Earth.

“Weightlessness” in orbit is not the absence of gravity but the prevalence of free-fall. Astronauts and spacecraft are both falling around Earth together; there is no normal force from a floor to announce their weight. Remove the supporting contact and you silence the sensation of weight even while gravity remains strong. Elevators, roller-coasters, and parabolic flights are terrestrial hints of the same principle: adjust the contact forces and you edit the feeling of weight.

Work and Energy

Force speaks locally; energy speaks globally. When a force acts through a displacement, it does work, W equals the integral of F right arrow times d s right arrow, and the work–energy theorem says that the net work equals the change in kinetic energy, normal triangle K. For many forces it is useful to invent a book-keeping quantity called potential energy whose changes record the accumulated work done by those forces. Near Earth we write U sub g almost equals m g of h relative to a chosen zero level; for an ideal spring we write U sub s equals one half k x squared, where x measures the compression or stretch. When only such conservative forces are at play, the sum K plus U remains constant. The path in between does not matter; only the endpoints do.

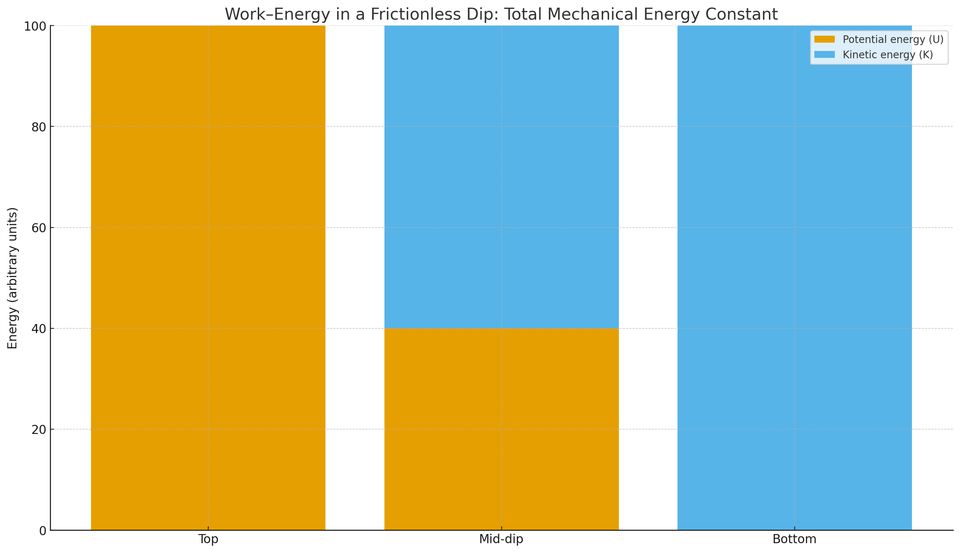
This global view can solve problems quickly. Imagine a puck sliding without friction into a spring and coming momentarily to rest at maximum compression. At the start the energy is purely kinetic, one half m v sub 0 squared; at the end it is purely spring potential, one half k x sub max squared. Setting them equal yields x sub max equals v sub 0 the square root of m divided by k with no attention paid to the intricate deceleration along the way. In roller-coaster intuition, a cart that drops by a height h in a frictionless dip gains speed v equals the square root of 2 g of h regardless of the track’s shape.

When dissipative forces like kinetic friction or air drag are present, mechanical energy alone is not conserved; some of it becomes thermal energy or sound. Yet the work–energy theorem still guides us: the non-conservative work modifies the energy balance by an amount equal to its algebraic sum. Energy is an honest accountant even when the world is messy.

Momentum and Impulse

Where energy summarises “how much ability to move” a system has, momentum tells us “how much motion” it carries and in which direction. Momentum is defined p right arrow equals m v right arrow. A force applied over a time produces impulse, J right arrow equals the integral of F right arrow of d t, and impulse changes momentum by normal triangle p right arrow equals J right arrow. This perspective makes short, intense forces intelligible: a bat’s brief strike on a ball imparts a large impulse and therefore a large change in momentum even though the contact lasts only milliseconds.

In the absence of a net external force, the total momentum of a system is conserved. Two carts on a low-friction track illustrate the point. If a moving cart gently collides elastically with an identical cart at rest, the first slows to a stop while the second takes off with the original speed; we see momentum transferred rather than created or destroyed.

In perfectly inelastic encounters the carts latch together and depart at a shared speed determined by momentum conservation; kinetic energy decreases, the deficit reappearing as thermal energy and deformation. In two dimensions the same rule governs billiard balls, curling stones, and even rockets expelling exhaust. Recoil and thrust are momentum stories.

The centre of mass (COM) acts as a faithful book-keeper. For an isolated system, the COM moves as if all the mass were concentrated there and all external forces were applied to that single point. Internal pushes and pulls between parts cannot nudge the COM because the third law balances them.

Symmetry → Conservation (A Teaser of Noether)

Patterns that refuse to change hint at hidden order. When the laws of physics do not depend explicitly on time, a quantity called energy remains constant. When the laws do not depend on position, momentum remains constant. When they do not depend on orientation, angular momentum remains constant.

Emmy Noether proved the profound theorem that ties these threads together, but you do not need the formalism to feel the truth. If the rules are the same today as yesterday, nothing in the rules can mysteriously add or subtract energy just because the clock advanced. If the rules are the same here as there, motion cannot gain or lose momentum simply by translating the scene.

A practical example wears humble clothes. Push off a solid wall while standing on a skateboard. The wall exerts a force on you; you exert an equal and opposite force on the wall. You glide backwards; the Earth glides imperceptibly forward. The total momentum of you-plus-Earth remains unchanged. Symmetry is not decoration; it is structure.

Confusions That Fade With Practice

Mass vs. weight.
Mass measures inertia and doesn’t change when you travel. Weight is the gravitational force on that mass, so it changes with the local field. A bathroom scale reads the normal force from the floor; in an elevator accelerating upward, that reading increases even though your mass does not.

Action–reaction pairs.
They do not cancel the net force on one object because each force lives on a different free-body diagram. The floor pushes up on you while gravity pulls you down; those determine your acceleration. The equal-and-opposite forces you exert on the Earth belong to the Earth’s diagram.

Normal force.
It isn’t a fixed m g. It adjusts to meet contact constraints. On a slope, a resting block has N equals m g of cosine theta. In a roller-coaster dip, N can exceed m g at the bottom and drop below m g at the top as the track supplies the needed centripetal acceleration.

Friction.
Static friction does “whatever is needed” to prevent slipping—up to a maximum. Once sliding begins, kinetic friction is usually smaller and roughly constant. That’s why a gently tilted block stays put until a threshold angle, then starts—and keeps—moving.

Balanced forces.
”Balanced” means zero acceleration, not zero velocity. A puck gliding at constant speed experiences zero net force even while it’s moving. Balance tells you about changes in motion, not motion itself.

A Snack of Calculus

Two tiny calculations repay the effort. First, suppose the acceleration is constant. The velocity as a function of time is v of t equals v sub 0 plus a t. The displacement during a time t is the area under the velocity–time graph: a rectangle v sub 0 t plus a triangle one half a t squared, yielding normal triangle s equals v sub 0 t plus one half a t squared. Eliminating time between v equals v sub 0 plus a t and this expression gives v squared equals v sub 0 squared plus 2 a times normal triangle s, a formula that often appears in kinematics tables but now arrives with geometric meaning.

Second, tie this to energy. In one dimension with constant mass, F equals m a and a equals d v divided by d t. Multiply both sides by d s and use v equals d s over d t to write F of d s equals m times d v over d t d s equals m times v times d v. Integrate from start to finish to obtain the integral of F of d s equals one half m v sub f squared minus one half m v sub i squared, which is the work–energy theorem in compact form. The algebra is modest; the concept is large. Work changes kinetic energy, and conservative forces let us represent that change as the difference of a potential function.

Try This at Home

A bottle Atwood machine turns kitchen supplies into a laboratory. Tie two identical empty bottles to the ends of a string that passes over a smooth door-edge or a pulley. Add water to one bottle and release. The heavier side descends while the lighter ascends. By timing several floor-to-ceiling runs with a phone stopwatch and measuring the distance, you can estimate the acceleration. Vary the mass difference and watch acceleration scale with it; extrapolate to infer g.

A phone-accelerometer push turns everyday furniture into an experiment. Place a phone on a sturdy chair and record acceleration with a free sensor app. Push the chair steadily for a few seconds and then stop. You will see a plateau during the push—evidence of approximately constant net force—and sharp spikes at the start and stop where impulses change the momentum more abruptly. The data will be noisy; the pattern will be unmistakable.

A rolling-chair push-off makes the third law visceral. Two people sit on wheeled chairs facing each other, feet planted. They press their palms together and push briefly. Both glide backward. Equal and opposite forces acted during the short contact, imparting equal and opposite impulses. If the masses are different, the lighter chair acquires a higher speed so that total momentum remains zero relative to the floor. Safety is part of the setup. Choose smooth floors, keep speeds low, give yourselves room, and prefer gentle impulses over heroic ones. Helmets matter if the wheels are skateboards instead of chairs.

A Friendly Mini-Glossary

• Inertia — The tendency of a body to maintain its state of motion unless acted upon by a net external force.

• Force — A vector interaction that changes velocity (produces acceleration). SI unit: the newton, kg times normal m divided by normal s squared.

• Net force — The vector sum of all external forces on the object you are analysing.

• Inertial frame — A reference frame in which Newton’s first law holds without introducing fictitious forces.

• Work — The path integral of the component of force along displacement: W equals the integral of F right arrow times d s right arrow.

• Energy — A scalar bookkeeping quantity. In mechanics we track kinetic energy K equals one half m v squared and potential energies such as m g of h or one half k x squared.

• Momentum — The product p right arrow equals m v right arrow; conserved for an isolated system.

• Impulse — The time integral of force, J right arrow equals the integral of F right arrow of d t, equal to the change in momentum normal triangle p right arrow.

• Conservative force — A force for which work depends only on start and finish, allowing a potential function U (with F right arrow equals negative nabla U).

Reflection and a Gentle Exercise

There is a moral hidden in the mathematics: arrangement beats effort.

We do not win by pushing harder but by seeing more clearly—choosing axes that align with the problem, reducing friction where it matters, and shaping paths that let energy do the bookkeeping for us.

Try this, slowly and attentively. Sketch a free-body diagram for each scene below. In every case, name what is changing and what is not. Where does the net force point? What, if anything, is conserved over the brief moment you examine?

Book on a shelf. Identify weight and the supporting normal. Ask whether anything is accelerating. If not, the forces balance; if the shelf flexes, the balance shifts but the story stays the same.

Person in a lift just beginning to rise. Watch the scale reading jump. The normal force briefly exceeds m g while the acceleration is upward, then settles once the speed becomes steady.

Car taking a bend at steady speed. Speed is constant but velocity is not. The net force points toward the centre of the curve; tyres provide the lateral friction that supplies the required centripetal acceleration.

The answers matter less than the habit: isolate, read, and reason.

Closing

We began with a promise: not description, but cause. The promise holds. Newton’s laws turn motion from spectacle into structure.

Once you see the grammar—forces as verbs, mass as resistance, energy and momentum as invariants under symmetry—the world reads differently. Doors push back. Ramps translate weight into along-slope pull. Coasting is not laziness; it is law.

In Part 4 we will meet the first cracks in the clockwork and learn how anomalies point the way to richer theories. For now, practise the grammar, and let arrangement do the heavy lifting.